Cheat Sheet
Lab Summary
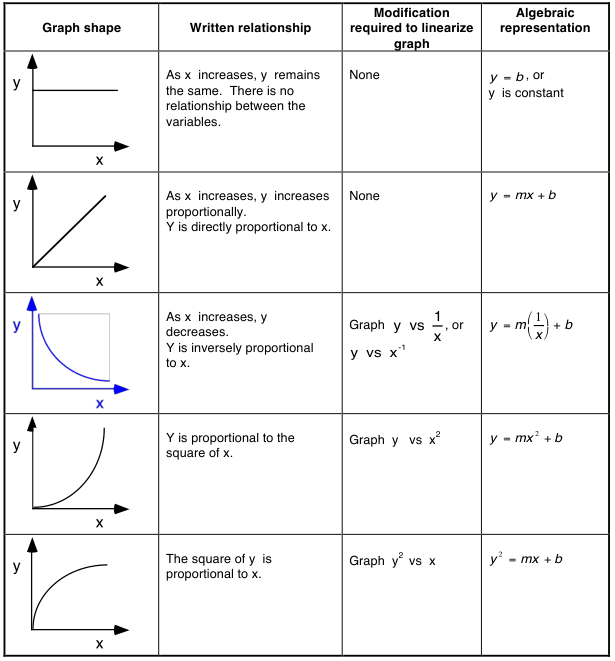
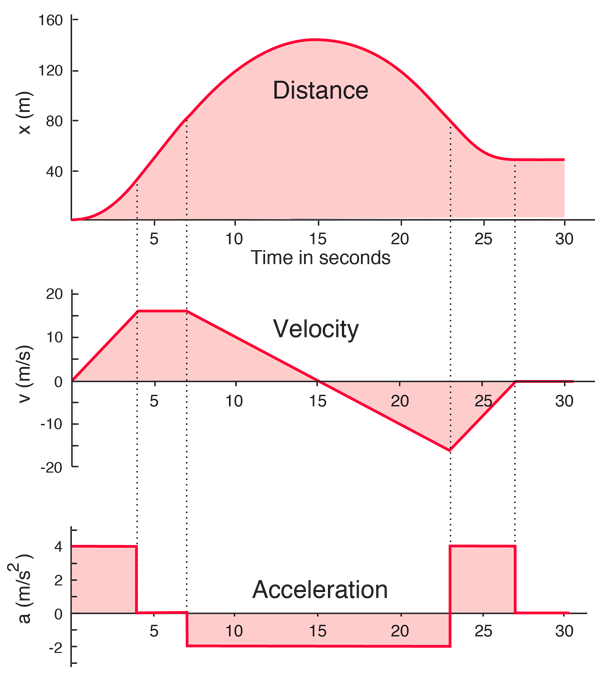
- Slope of the Velocity vs. Time graph is acceleration
- Acceleration is measured in m/s/s or m/s
- Slope of the Position vs. Time
General Mathematical Models:
-
For this lab (with no initial position or initial velocity):
-
For an object with an initial velocity and initial starting point:
Defintions & Notes
- Displacement indicates how far an object ends up from its initial position, regardless of its total distance traveled.
- Average velocity is displacement divided by the time interval over which that displacement occurred. Slope of position time graph over a time duration.
- Instantaneous velocity is how fast an object is moving at a specific moment in time. Slope of position time graph at a specific time.
- Acceleration tells how much an object’s speed changes in one second.
- When an object speeds up, its acceleration is in the direction of motion.
- When an object slows down, its acceleration is opposite the direction of motion.
Thinking about graphical relationships
Position-time graphs
- To determine how far from the detector an object is located, look at the vertical axis of the position-time graph.
- To determine how fast an object is moving, look at the steepness (i.e. the slope) of the position-time graph.
- To determine which way the object is moving, look at which way the position-time graph is sloped.
- A position-time slope like a front slash
/ means the object is moving away from the detector.
- A position-time slope like a back slash
\ means the object is moving toward the detector
- Instantaneous velocity is found by taking the slope of the tangent line to a position-time graph
Velocity-time graphs
- To determine how fast an object is moving, look at the vertical axis of the velocity-time graph.
- To determine which way the object is moving, look at whether the velocity-time graph is above or below the horizontal axis.
- An object is moving away from the detector if the velocity-time graph is above the horizontal axis.
- An object is moving toward the detector if the velocity-time graph is below the horizontal axis.
- To determine how far an object travels, determine the area between the velocity-time graph and the horizontal axis.
- On a velocity-time graph it is not possible to determine how far from the detector the object is located.
- Most everyday motion can be represented with straight segments on a velocity-time graph.
Acceleration
- Negative Acceleration does not always mean slowing down
- Negative Acceleration means the velocity is changing in the negative direction
Acceleration: Increasing vs. Decreasing Speed
- Speeding Up: Acceleration and velocity have the same sign
- Slowing Down: Acceleration and Velocity have opposite signs
Shapes of Graphs
Shapes of Graphs

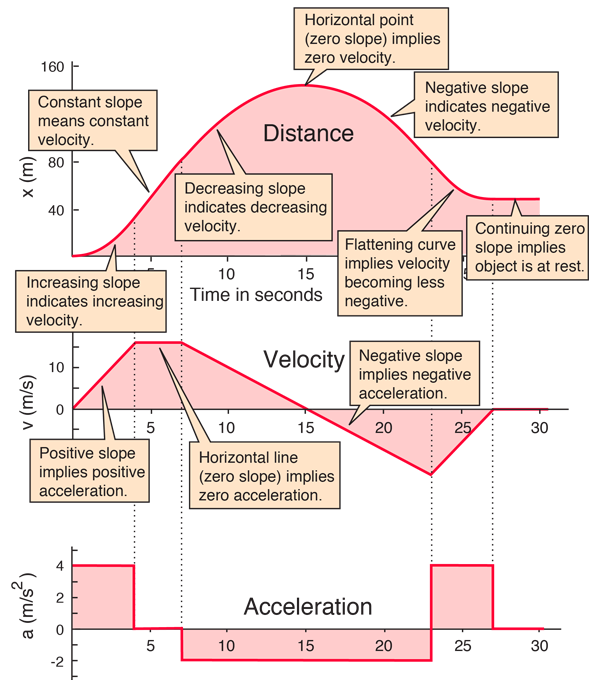
Shapes of Graphs - Summary
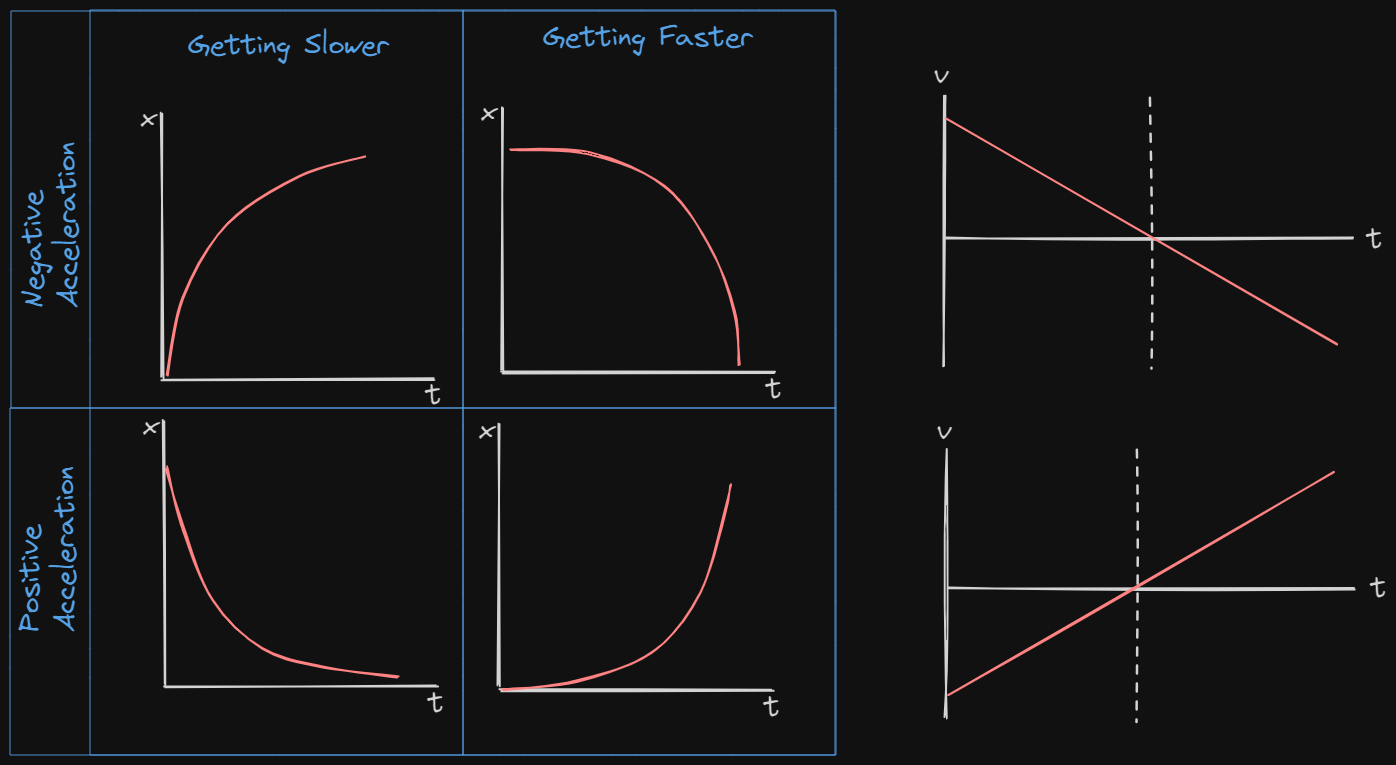
VT Graphs
For each object...
- Determine the displacement between
- Determine the average acceleration during the first
- Describe the motion in words.
- Draw the position vs. time graph that goes with the VT Graph.
VT Graph 2
- Give a written description of the motion.
- Determine the displacement of the object from
- Determine the displacement of the object from
- Determine the displacement of the object from
- Determine the object’s acceleration at t = 4 seconds.
Physics is more than plugging numbers into equations!
Solve 



A poorly tuned car accelerates from rest to a speed of 28 m/s in 20 seconds. What is the acceleration of the car? How far does the car travel in this time?
 Remember to:
Remember to:
- Sketch and Translate
- Simplify and Diagram
- Represent Mathematically
- Solve + Evaluate
 Hint:
Hint:
Use a graph or graphs to solve the problem.
Multiple Representations:
- Verbal: Describes the motion of the car in a narrative manner.
- Pictorial: A picture shows the initial and final motion of the car.
- Diagrammatic: The picture is simplified and shows the motion of the car over multiple clock readings.
- Graphical: Three representations that show how the position, velocity, and acceleration of the car vary over time.
- Mathematical: Describes the velocity of the car as a function of time and the position of the car as a function of time.
Problem Solving Process:
- Sketch and Translate
- Simplify and Diagram
- Represent Mathematically
- Solve + Evaluate
1. Sketch
- A sketch of the object or objects at the beginning of the motion, at the end of the motion, and any important points in between where the motion changes (i.e. if the acceleration of the object changes).
- A coordinate system Label the axes and the origin (position 0).
- Symbols that represent the time, position, and velocity of each object at each moment you have draw above. Use subscripts to depict different times and different objects (i.e.
- Draw arrows to show the acceleration and velocity of the object between each position (or write
1. Translate
Now that you have a sketch of the situation you should organize everything you know and want to find. Therefore you should:
- Make a table listing all of the symbol values that are known for the problem or that can be determine from simple geometry. Check that the signs are consistent with your sketch and its coordinate system. Also list known relationships, such as
- Make a list of the unknown quantity or quantities you'll need to answer the question.
2. Simplify and Diagram (Physics Diagrams)
- From our sketch we will no create physics diagrams...for motion this includes:
- position vs. time graph
- velocity vs. time graph (most useful)
- acceleration vs. time graph
3. Represent Mathematically
- mathematical description of the process
- turn physics diagrams into equations:
- use area of v-t to calc displacement
- use slopes to calculate velos, or accelerations
- use position functions to find final positions
4. Solve + Evaluate
- substitute in given quantities and solve!
- Evaluate: does this number make sense? Is it a reasonable solution?
Example:
A poorly tuned car accelerates from rest to a speed of 28 m/s in 20 seconds. What is the acceleration of the car? How far does the car travel in this time?
Sketch and Translate

Simplify and Diagram
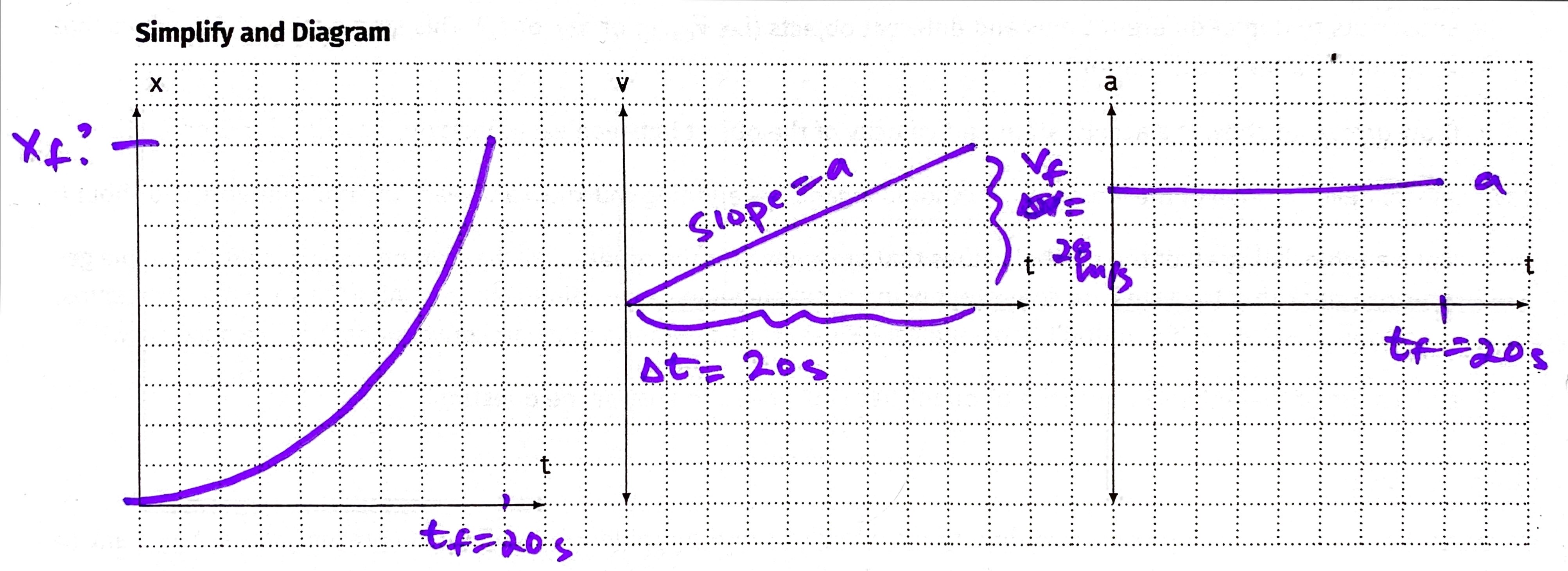
Represent  Solve:
Solve:

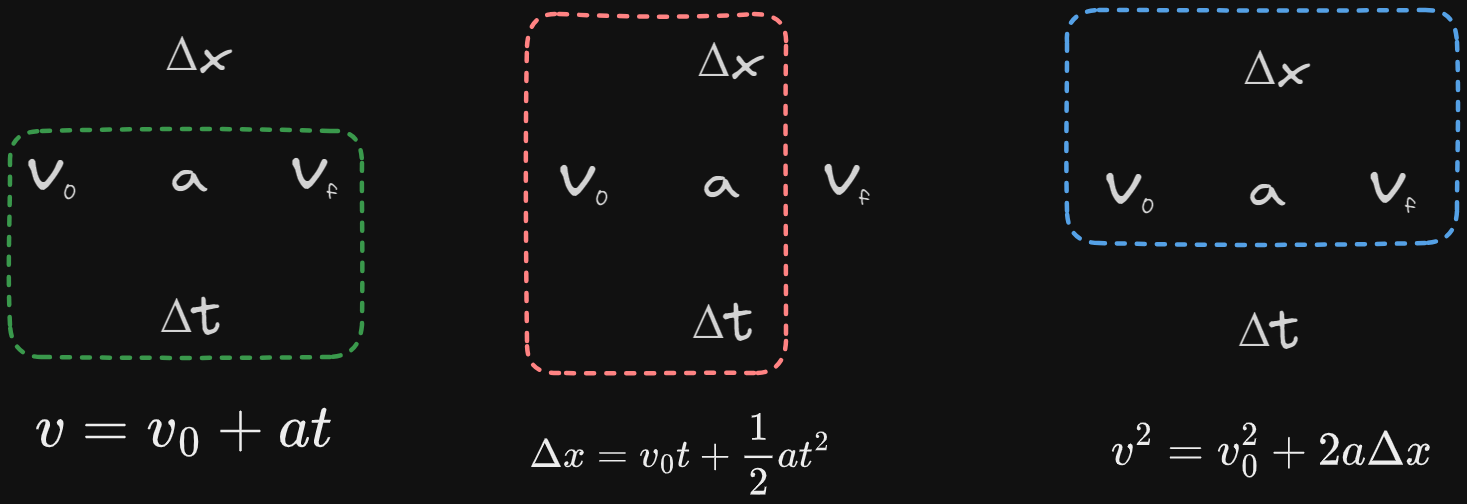
Kinematic Equations
...from AP Reference Table
- the
- we will often remove that subscript when writing equations involving problems with only one plane of motion: i.e.
Kinematic Equations
Reminder:
so...
Kinematic Cross Diagram for Problem Solving

Kinematic Cross Diagram
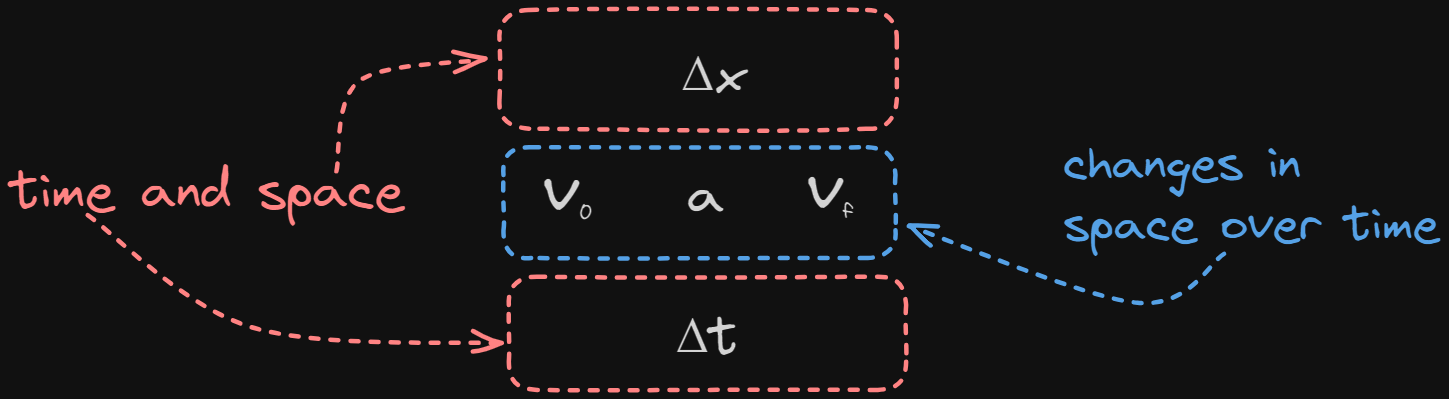
Identifying Equations
Non-reference Table Equations
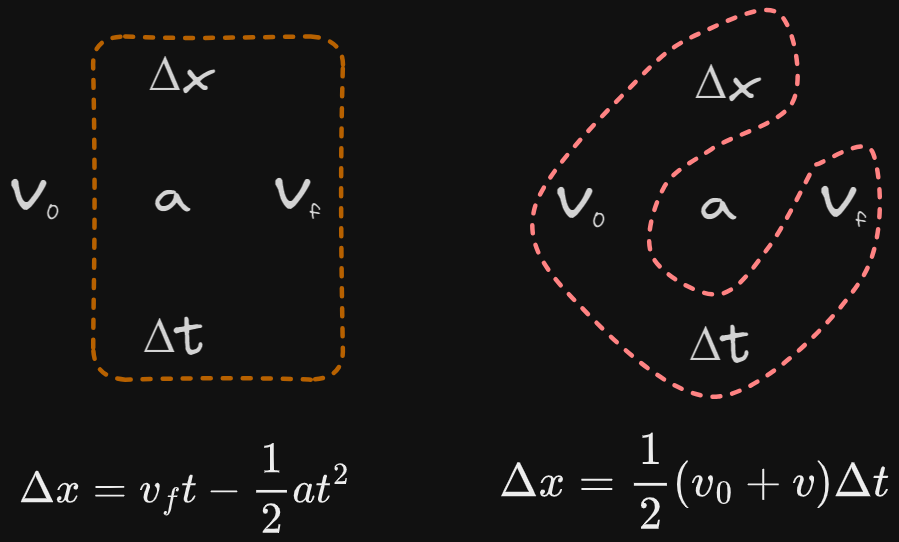
Using the Cross Diagram
- Setup
- Write down the cross
- Write down the known variables and underline those variables in the cross
- Star (or circle) the variable that is unknown and is being solved for
- Planning
- Circle the variables that are involved in this problem
- Use the equation that involves those four variables
- Execution
- Solve the problem
- You can circle twice: solve for first unknown to use in second equation
Example
A poorly tuned car accelerates from rest to a speed of 28 m/s in 20 seconds. What is the acceleration of the car? How far does the car travel in this time?
More Complicated Example
Gideon is South's best speed skater. He accelerates from 0.00 m/s to 7 m/s in 5 s and then continues at this constant speed for another 8 s. What is the total distance Gideon skates?
Practice
A speedboat increases its speed from 14.3 m/s to 31.1 m/s in a distance of 274 m. Determine the time over which this acceleration occurs.
