Angular Velocity
- Measure of how fast an object is rotating.
- Symbol:
- Is equal to the change in angular displacement in a time.
- measured in rad/s
Angular and Linear Velocity
Angular velocity is analogous to linear velocity, and we can determine their relationship.
-
-
so
-
sub in:
Angular Acceleration
- measured in rad/s/s or rad/s
Translating Between Linear and Angular
How to translate the two (not on the reference table!)
| Linear | Angular |
|---|---|
Rotational Kinematics:
The same as linear, but with their rotational twin!
| Linear | Angular |
|---|---|
Torque
When a force has the ability to rotate an object
- i.e. Pushing the edge a door so it rotates around its axis of rotation (the hinges)
Torque
Depends on:
- where the force is exerted
- how large the force is
- what angle the force is at
Torque
Balacing Act:
Task 1
Add masses to each side of the rod so that the rod does not rotate, but is balanced (parallel to the table). In particular, add two masses to one side and one mass to the other side. Is there more than one arrangement that will balance the rod? Explain.
Task 2
Draw a Free Body Diagram for your setup in task 1. Are the forces balanced?
Balacing Act:
Task 3
Would the diagram that Mr. Porter drew on the board rotate? (Draw a FBD for the situation...does the net force explain the situation?)
Task 4
Where could we place a mass in the previous question so that the ruler would not rotate?
Balacing Act:
Task 5
Develop a method to determine the mass of your meterstick using the balance.
Notes 

Extended Bodies
- Rigid (parts of object do not move with respect to each other)
- nonzero size
Balance your
pencil 
on your finger
The balance point
is the pencil's
center of mass.
Center of Mass
The point on an object where a force exerted on the object pointing directly toward or away from that point, will not cause the object to turn. The location of this point depends on the mass distribution of the object.
Center of Mass
The average location of all of the mass of an object.
Center of Mass:
For a 1-dimensional case with objects along a line, this simplifies to:
Static Equilibrium
- Object remains at rest
- Sum of forces = zero (balanced forces)
- Sum of torques = zero (balanced torques)
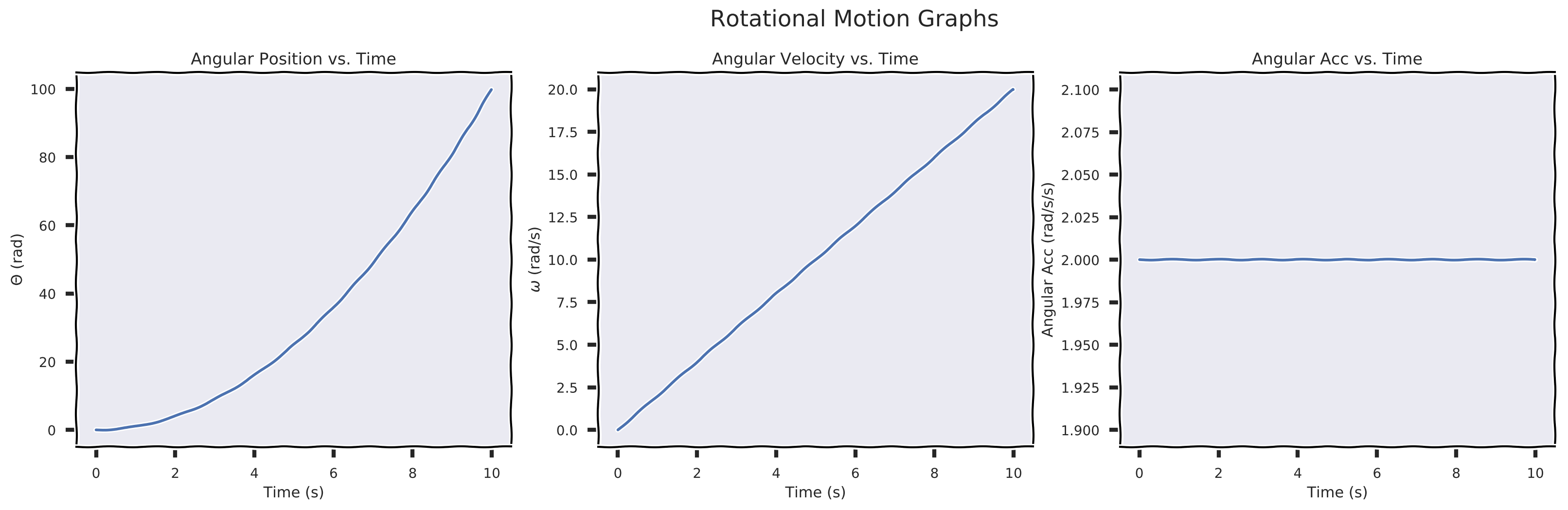
Consider the beam shown below to be in equilibrium (Net Torque = 0) around the fulcrum at Point A. The mass of the beam is 6.5 kg, the mass of the resting mass is 43 kg, and the distance between vertical yellow marks is 49 cm.
What is the magnitude of force F?
Physics Classroom Practice
AP Workbook
A long rod of length L and negligible mass supports a box of mass M. The left end of each rod is held in place by a frictionless pin about which it can freely rotate. In each case, a vertical force is holding the rods and the weights at rest. The rods are marked at half-meter intervals.
7.B
A. Rank the magnitude of the vertical force
B. Sketch the forces acting on the rod-box system
7.B
C. In which cases is the force from the pin up? Down? Zero? Justify your answers.
Example with Angle
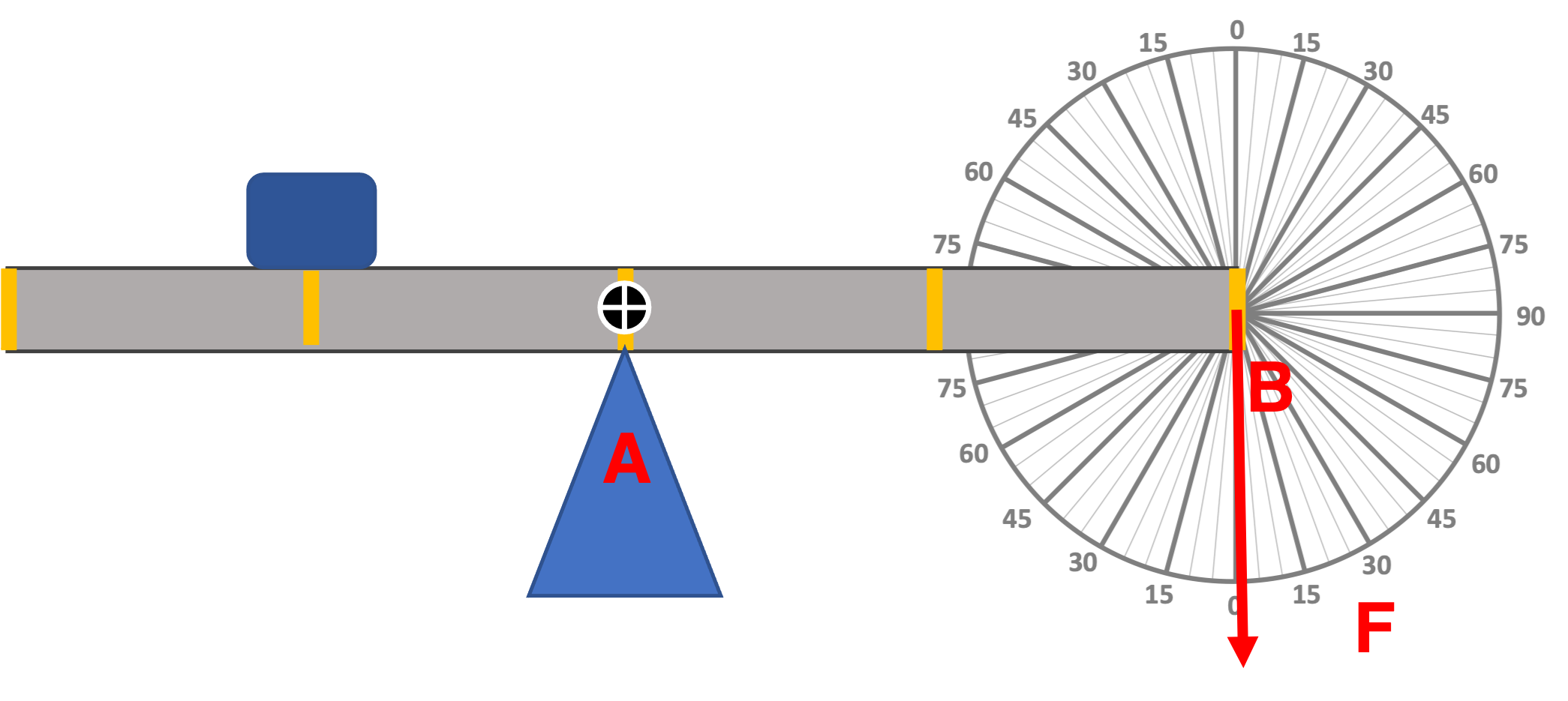
Consider the beam below in equilibrium supported by a pin joint at A and a rope attached from the end of the beam to the pin joint at point B. The mass of the beam is 39.0 kg, the mass of the person is 43 kg, and the distance between vertical yellow marks is 1.6 meters. Pin joints can provide forces in the horizontal and vertical directions to maintain equilibrium.
- Tension in Rope
- Forces x, y at A
- Forces x, y at B
Translate
Physics Ideas:
- Equilibrium
- Balanced Torques
- Balanced Forces
Givens
- mass:
- levers:
Unknowns
Physics Diagrams - Force Diagram
Solving Process
- Use sum of Torques to find Tension
- Use Tension and sum of forces to find forces at Pivot Point A
- Use above information for Pivot Point B
Represent Mathematically
Sum Torques
Horizontal Forces
And Vertical Forces
Unbalanced Torque
Causes rotational (angular) acceleration!
Newton's Second Law Rotation
angular acceleration
Net Torque
Moment of Inertia (rotational mass equivalent)
What is Moment of Inertia?
Demo:
- Twisting Rod (where is it easiest to hold the rod to twist it?)
Moment of Inertia
Why does the skater spin faster when she brings in their arms?
Moment of Inertia
- the rotational analog of mass for linear motion
- it is related to the mass and the location of the mass
- closer the mass is to the rotational axis, the lower the moment of inertia (easier to spin)
- for a point like object
- this relationship is used to build the equations for other moments of inertia
Reference Table
moment of interia
mass
position vector magnitude
Example
A potter is shaping a bowl out of clay on a potter's wheel initially rotating at a constant angular speed of 22.4 rad/sec. A 1.40-N friction force between her hands and the clay slows the system to a stop. The wheel is a 11.5-kg disk with a radius of 26.2 cm. The bowl has a moment of inertia of 0.074 kg•m
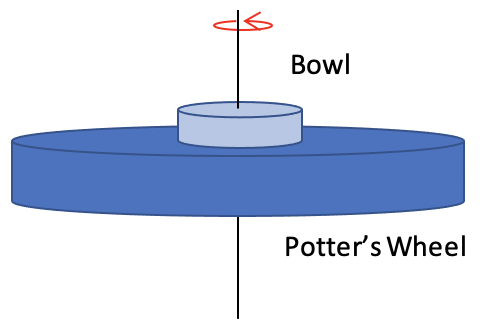
- What is
- What is total
- What is the
- What is
Example
A block of unknown mass is attached to a long, lightweight string that is wrapped several turns around a pulley on a horizontal axis through its center, as shown. The pulley is a uniform solid disk of mass
Class Work:
On your own:
Together:
- 7.E
- 7.G
Parallel Axis Theorem
New Moment of Interia
Moment of interia about original axis
Mass
Distance between two axes
Example:
The symmetrical object shown in the figure is made of a material with uniform density and the object has mass
In terms of momentum, why does the water rocket increase its velocity?
Angular Momentum
Angular Momentum
- Before calculating angular momentum, it is necessary to define a rotational axis.
- The angular momentum
Conservation of Momentum
- Angular Momentum is conserved if there is no net torque on the system
- Unlike energy, angular momentum is conserved separately from linear momentum. (Do not combine them in a single equation)
- Angular momentum is a vector – angular momentums in the same sense add, angular momentums in opposite senses subtract.
Conservation of angular momentum:
- Conservation of Angular Momentum is used when a translating object interacts with a rotating one.
- Examples: Throwing a ball from a merry-go-round, bat hitting a baseball.
- Conservation of Angular Momentum is also used for a single rotating object changing shape.
- Example: A figure skater pulls in her arms. Moment of inertia decreases so angular velocity must increase to keep angular momentum constant.
Impulse
- The impulse-momentum theorem can be written for angular momentum, too.
- A change in angular momentum equals the net torque multiplied by the time the torque is applied.
Series of Angular Momentum Gifs
Animation for Moment of Inertia
Kinetic Energy
The kinetic energy for a moving particle:
relating its linear speed and angular velocity:
Thus,
Explain Using Energy
A solid sphere rolls without slipping along a track shaped as shown at right. It
starts from rest at point A and is moving vertically when it leaves the track at
point B.
At its highest point while in the air, will the sphere be (a) above, (b) below,
or (c) at the same height as point A? _____
Explain your reasoning.
In each case, a 1-kg object is released from rest on a ramp at a height of 2 m from the bottom. All of the spheres roll without slipping, and the blocks slide without friction.
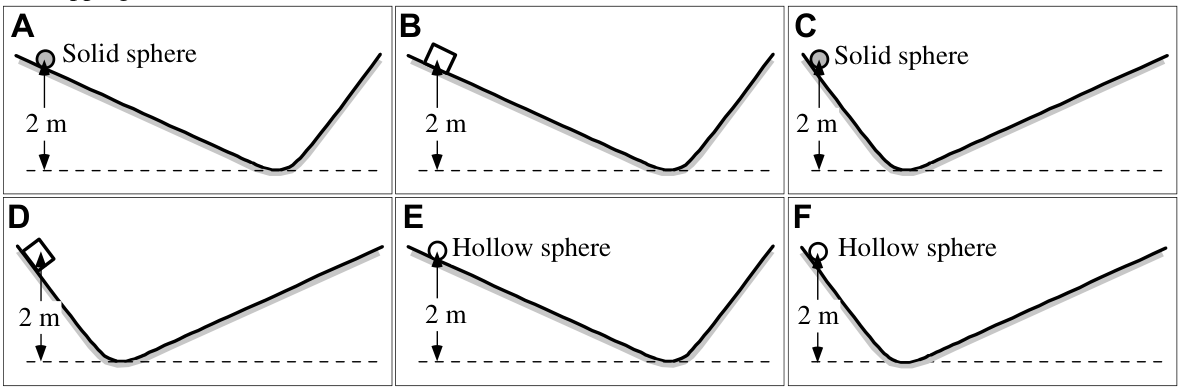
Rank the maximum height of the objects on the other side of the ramp.
Explain your reasoning
In each case, a 1-kg object is released from rest on a ramp at a height of 2 m from the bottom. All of the spheres roll without slipping, and the blocks slide without friction. The ramps are identical in Cases A and C. The ramps in Cases B and D are identical and are not as steep as the others.

Rank the speed of the objects when they reach the horizontal surface at the bottom of the ramp.
Explain your reasoning.
Four objects are placed in a row at the same height near the top of a ramp and are released from rest at the same time. The objects are a 1-kg solid sphere; a 1-kg hollow sphere; a 2-kg solid sphere; and a 1-kg thin hoop. All four objects have the same diameter, and the hoop has a width that is one-quarter its diameter. The time it takes the objects to reach the finish line near the bottom of the ramp is recorded. The moment of inertia for a solid sphere is
Rank the four objects from fastest (shortest time) down the ramp to slowest.
Rolling Race
How do different equations for